Collections are an integral part of almost any application that we build or maintain as software engineers. The concept of traversing collections with a for-loop is often one of the first paradigms learned by new engineers. Collection-like objects exist in most, if not all, languages. In C# we have several options when it comes to collections and each option comes with tradeoffs. As software engineers, it is our job to choose the right tool for the job. The decision of what kind of collection to use for a given scenario needs to consider the context in which the collection will be used. We should ask ourselves Will the collection be iterated, searched, or manipulated heavily in the most common use cases? The collection type we choose for a given scenario could have massive performance impacts on the application and its users.
We will focus on a few collection types in C# to determine how they perform in regard to Big O notation when searching for and manipulating elements of each collection type. This post doesn't require you to be an expert in Big O notation, but it does assume a basic understanding of the topic. I will be focusing on the following collection types.
List<T>Dictionary<TKey, TValue>&HashSet<T>- Sorted collections
There are many other collection types that could be covered, but I wanted to focus on the types that I've used and seen most in my career. If you're interested in learning more about the Big O notation in regard to other .NET collection types, I would highly encourage digging into it for yourself!
List<T>
I would consider List<T> to be the most commonly used collection type in the .NET ecosystem. That means we should understand how we can use it effectively and its performance when carrying out certain tasks. In terms of Big O notation, I'd say that most List<T> operations can be expected to be linear or O(n). A linear algorithm's runtime is directly affected by the size of the input being processed. As the input size grows the runtime should grow linearly proportional to the input growth.
Manipulating lists
Manipulating a collection is a common operation and typically involves adding or removing items from the collection. Normally the add and remove functionality is a linear operation. Below is a screenshot of benchmark results adding a random number to a List<T> at increasing sizes. As the size of the list grows, the mean runtime also grows nearly linearly.

While typically list manipulation runtimes are linear, there is an exception when adding to lists. When a list is created, there is an overloaded constructor that accepts an integer to indicate the Capacity of the list. If we create a list with a defined capacity and the Count property at the time of adding is less than the Capacity, then adding to a list is O(1) or constant time. The reason for this is that the underlying array does not need to be expanded to accommodate the new element. This means that the speed of the operation is not affected by the size of the input (in this case the size of the collection). We can see this in action in the benchmarks below. As the input size grows linearly, the runtime of adding an element to the list remains constant.
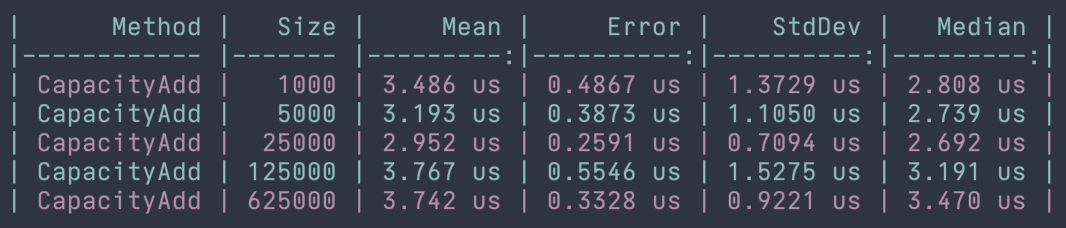
Searching lists
When working with collections we often need to search the collection for a particular element. This could be with .Find, .Contains, .IndexOf, .Where, and other methods that look for a particular element in a collection. For this reason, it's important to understand that the runtime of searching for an element in a list is also O(n) or linear. The algorithm to find an element most likely needs to iterate through each element to find the one that it is looking for. In the worst-case scenario, the item isn't in the list and we've had to look at every element. We can see this in the benchmarks below using the .Find method to find a specific element in a list.
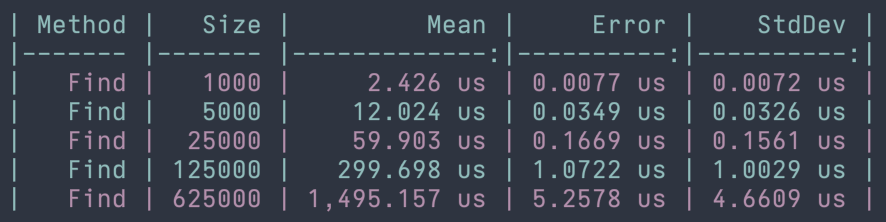
Dictionary<Tkey, TValue> and HashSet<T>
In this section, we are going to focus on a couple of hash-based collection types, which are Dictionary<TKey, TValue> and HashSet<T>. While these are different types they both rely on hashing algorithms to store and keep track of the elements that are contained inside their collections. As we look at manipulation and searching operations we'll see some similarities with List<T>, but there are also some key differences that make these hash-based types appealing in certain scenarios.
Manipulating hash-based collections
Both Dictionary<Tkey, TValue> and HashSet<T> are unsorted collection types, just like List<T>. We can also expect these hash-based collections to perform similarly to lists when it comes to manipulating elements. The documentation states that when adding items from a dictionary or hash set without a defined Capacity, the operation will have a linear, or O(n), runtime. If we have defined a value for Capacity and the Count value is less than the capacity when adding, the operation will be performed in constant time or O(1).
Interestingly enough when I performed benchmarks of this data, I noticed that the Add method performed almost identically when explicitly setting the capacity and when not. I took a look at the source code for the Dictionary class here, which was quite interesting but a little challenging to follow while navigating in GitHub. For the dataset and benchmarks the Add method was performed in constant time.
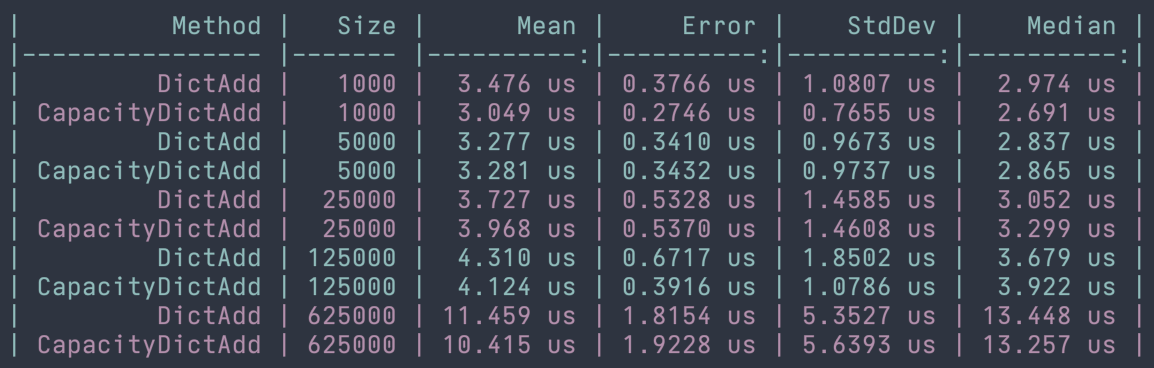
When it comes to removing elements from a dictionary or hash set, the operation is always performed in constant time. The reason for this is that the stored hashed values can be easily found in the underlying hash table for each of these collection types. Let's take a look at some benchmarks that confirm these behaviors and their runtimes. The example below shows the benchmark results for removing elements from HashSet<T>.
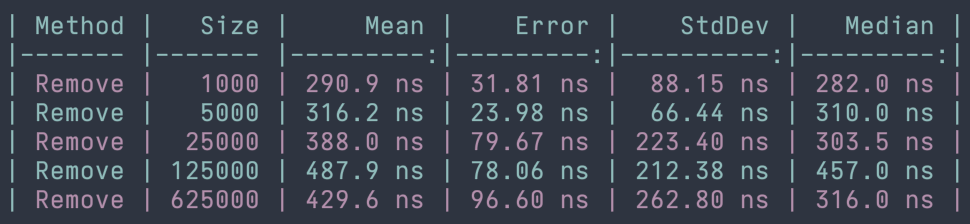
Searching hash-based collections
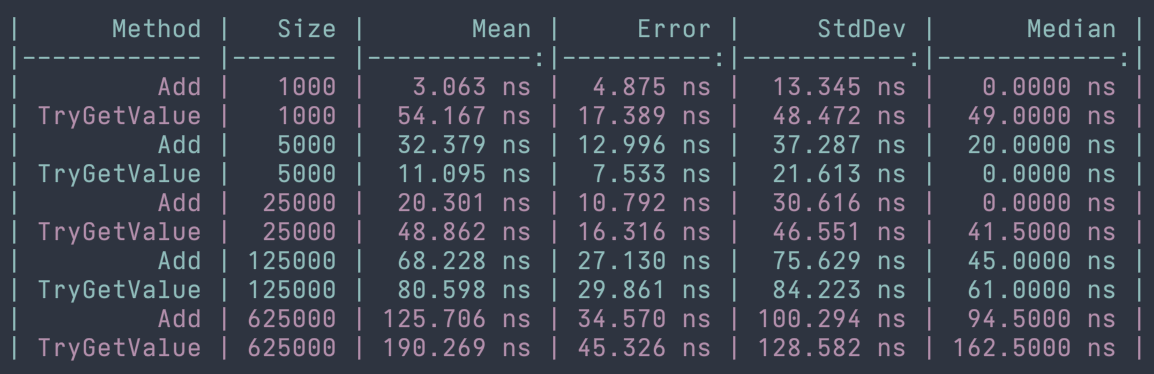
We've seen some of the efficiencies that we can gain from using hash-based collections when manipulating data. Now we're going to look at their performance when searching for specific elements. There was one operation that we discussed previously that may provide a tip as to what the search performance might be...and that was the Remove operation. If we think about what needs to happen to remove an element from a hash-based collection, we first need to find the element, then we need to remove it. Searching is essentially the same operation without the removal, so if you remember that removal is performed in constant time we should be able to assume that searching is also performed in constant time or O(1). Fortunately, that's a correct assumption as we'll see the runtimes approaching constant time in the following examples. The examples will show indexing into a dictionary and also calling HashSet<T>.TryGetValue.
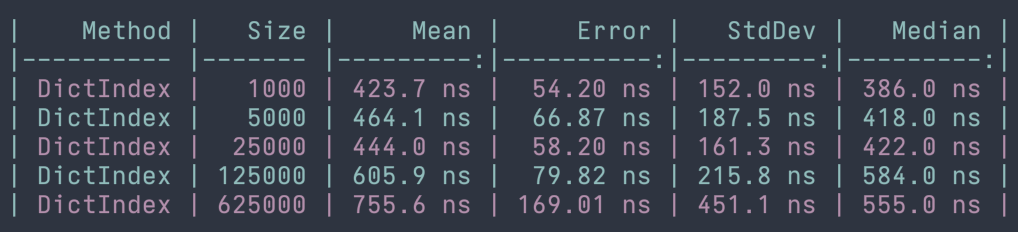

Sorted Collections
So far we've looked at List<T>, Dictionary<TKey, TValue>, and HashSet<T> and how they perform different actions through the lens of big O notation. I wanted to take a quick look generally at sorted collections and their runtimes for the operations we've examined for previous types. Those operations are adding, removing, and searching each of the collections. One similarity between sorted collections and the ones discussed already is that the runtime is still O(n) when the internal capacity of the underlying data structure needs to grow due to the operation.
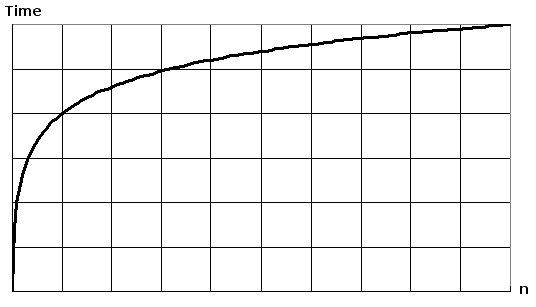
In most circumstances, we can expect sorted collections to perform operations in logarithmic time or O(log n). This means that the runtime does change as the input size grows, but less drastically as the input size continues to grow.
Although I haven't used sorted collections often in my day-to-day, I think it's useful to examine at least one benchmark to confirm their behavior, but also to be aware of their performance features. If there is a data set that we know will always be sorted, maybe it makes sense to use a SortedList<TKey, TValue> instead of a List<T>. Decisions always come with tradeoffs and being fully aware of the options and their implications is key to making the most correct decision. Let's take a look at the performance benchmarks for adding to and searching a SortedList<TKey, TValue> and confirm that we see close to logarithmic runtimes.
The goal of this post wasn't to share the runtimes for each of these operations on the different collection types. That can be found easily in the documentation. The main goal was to present this information in a way that highlights the performance features of each operation and type in given scenarios. With this information, we should be prepared to choose the correct collection for any problem that is thrown our way.
If you'd like to check out any of the benchmark code, head over to this repo. If I'm being honest this was my first introduction to BenchmarkDotnet and it was a great learning experience. While the benchmarks mostly represent the runtimes as expected, there may be some margin of error due to the way that the benchmarks had to be set up. Unfortunately performing very fast mutations isn't super simple to benchmark, so some of the setups for each benchmark run may be included in the executed times.